Doc. Torricelli
 
cronologia telegrafo
 
cronologia telefono
 
cronologia radio
 
cronologia TV
 
cronologia comp.
 
indice scienziati
 
bibliografia
 
  
Evangelista  Torricelli
 
     
DOCUMENTI
  
Biografia a cura di   Egidio Festa (1)
   

 
 
1. Infanzia e adolescenza
  

Le notizie sull'infanzia e l'adolescenza di Torricelli sono rare ed imprecise. Sappiamo con certezza che egli nacque a Roma il 15 ottobre del 1608. Disponiamo inoltre di indicazioni sulla sua formazione scientifica, grazie al contenuto di una lettera a Galileo dell'11 settembre 1632. In essa Torricelli spiega che dopo aver studiato da solo per due anni sotto la disciplina delli padri gesuiti, fu a diciott'anni scolaro dell'abate Benedetto Castelli.
Nel febbraio di quello stesso anno 1632 era stato pubblicato a Firenze il Dialogo sopra i due Massimi Sistemi del Mondo. Castelli - che fu, com'è noto, fra i più fedeli discepoli ed amici di Galileo - scrutava con affettuosa premura le reazioni degli ambienti romani al contenuto del libro. Costretto ad assentarsi per alcuni giorni, pregò Torricelli di fungergli da segretario. Il giovane scolaro ebbe così l'occasione di scrivere a Galileo, in risposta ad una sua missiva, e di informarlo dell'azione svolta dall'abate per evitare una precipitosa resoluzione , e cioè la condanna del libro e del suo autore. La speranza che si potesse evitare il peggio, non aveva ancora definitivamente abbandonato gli amici romani di Galileo.Torricelli, come egli stesso spiega in questa lettera, fu a Roma fra i primi lettori del Dialogo. Ne studiò il contenuto con quel gusto [...] che abbia avuto uno che, già havendo assai bene praticata tutta la geometria [...] et che havendo studiato Tolomeo et visto quasi ogni cosa del Ticone, del Keplero e del Longomontano , finalmente adheriva, sforzato dalle molte congruenze, al Copernico, et era di professione e di setta galileista.E' questa la sola occasione in cui Torricelli si dichiara apertamente seguace della dottrina copernicana. Egli fu senza dubbio profondamente scosso dalla sorte riservata al Dialogo e dalla condanna di Galileo emessa nel giugno del 1633 dal tribunale del Sant'Uffizio. Tanto più che Castelli - costretto ad allontanarsi da Roma nel momento stesso in cui si apriva il processo - gli aveva affidato l'incarico di seguire lo sviluppo degli avvenimenti e di tenerlo al corrente.
2. Presso Galileo ad Arcetri

Poco sappiamo dell'attività svolta dal giovane Torricelli nel corso degli anni compresi fra il 1632 ed il 1641. E' accertato ch'egli seguì Mgr. Giovanni Ciampoli nelle Marche, ove l'illustre prelato fu inviato come governatore dopo la condanna di Galileo. Ciampoli pagava con l'allontanamento da Roma l'amicizia e l'ammirazione che lo legavano da sempre all'autore del Dialogo.
Durante questo lungo periodo, Torricelli fu un attento studioso della teoria del moto, come è attestato da una lettera di Castelli a Galileo del 2 Marzo 1641. L'abate era stato autorizzato a recarsi presso Galileo, prigioniero nella sua villa d'Arcetri. Nel comunicare la buona nuova al Maestro, egli promette di portargli un libro, e forsi ancora il secondo libro, fatto da un mio discepolo [...] che ha dimostrato molte proposizioni di quelle De Motu dimostrate già da V.S., ma diversamente superedificando maravigliosamente intorno alla stessa materia[...]. Il discepolo è proprio Evangelista Torricelli tornato a Roma all'inizio del 1641. Il libro fu favorevolmente giudicato da Galileo, e Castelli, profondamente colpito dalla cecità e dagli acciacchi che affliggevano l'illustre ospite, temendo che le sue più recenti "speculationi" potessero andar perdute, gli propose di inviare a Firenze Torricelli per facilitarne la redazione. [Si veda il racconto di Vincenzio Viviani, trasmesso da Ludovico Serenai, in Torricelli, Opere, a cura di G. Loria e G. Vassura, Faenza, 1919, vol. I (1), p. VI]
La proposta di Castelli fu immediatamente accettata da Galileo, e due settimane dopo, il 27 aprile 1641, Torricelli scriveva al prigioniero di Arcetri per ringraziarlo dell'invito e rammaricarsi di non poter partire prima del rientro a Roma dell'abate. L'assenza di Castelli si protrarrà fino all'autunno, ed è permesso chiedersi se essa fu la sola causa della mancata partenza di Torricelli. Si può osservare che nel contesto politico e culturale dell'epoca, occorreva una buona dose di coraggio per andare a raccogliere le idee di colui che i potentissimi inquisitori del Sant'Uffizio volevano far tacere per sempre. Ed in effetti Torricelli, pur continuando a scrivere a Galileo, non dà nessuna indicazione precisa sulla data del suo arrivo, ed anzi sembra esitare sulla decisione stessa di trasferirsi a Firenze. Galileo se ne duole in una lettera del 27 settembre 1641. Dopo aver ringraziato Torricelli per avergli inviato un suo lavoro sulle spirali, così prosegue: (…) attribuirgli le meritate lodi non mi pareva che uno o due fogli ne fosser capaci, però mi riserbava a pagar tale ufizio e debito con V.S. in voce, stando sulle speranze d'aver pure a goderla per qualche giorno avanti che la mia vita, ormai vicina al fine, si terminasse. Dello adempirsi tal mio desiderio me ne dette V.S. in una sua amorevolissima non lieve speranza, ma ora non sento nell'ultima sua cenno di confermazione anzi, per quel che intendo nell'altra sua scritta al Padre Reverendissimo Castelli ed a me mandata aperta, ritraggo pochissimo o niente di vivo rimanere in tal mia speranza. Non voglio né debbo cercare di ritardare sì buoni incontri ed avvenimenti che meritatamente dovrebbono costì succedere al valor suo, tanto sopra le comuni scienze elevato; ma bene gli dirò con sincero affetto, che forse anco qua sarebbe riconosciuto il merito del suo ingegno peregrino, ed il mio basso tugurio non gli riuscirebbe per avventura ospizio men comodo di qualcuno de i molti sontuosi, perché son sicuro che l'affetto dell'ospite non lo ritroverebbe in altro luogo più fervente che nel mio petto; e so bene che alla vera virtù piace questo sopra ogni altro comodo.
Le parole di Galileo hanno un effetto quasi immediato: ai primi di ottobre Torricelli parte per Firenze. Qui redige, sotto la guida del venerando Maestro, la Quinta giornata da aggiungersi alle quattro dei Discorsi e dimostrazioni matematiche intorno a due nuove scienze, già pubblicati a Leida, presso gli Elzeviri, nel 1638.La morte di Galileo il 6 gennaio 1642, interrompe bruscamente l'attività di Torricelli, che decide di ritornare subito a Roma. E sta già per partire, quando Ferdinando II dei Medici gli propone di restare a Firenze col titolo di "matematico del Granduca di Toscana" e " Lettore di matematica" all'università di Pisa. Questa nomina, immediatamente accettata, segna l'inizio per Torricelli di un periodo di intensa attività, nel corso del quale maturano le soluzioni di numerosi problemi di matematica e di fisica.

Nei lavori di Torricelli possono essere individuate quattro diverse direzioni di ricerca, che coprono la quasi totalità degli argomenti trattati da Galileo, ad eccezione dell'astronomia. Nella prima - la Geometria - Torricelli ottiene risultati notevoli, in particolare, la quadratura della curva cicloidale e la cubatura dell'iperboloide di rivoluzione (solido iperbolico acuto). Egli utilizzò per primo gli indivisibili curvi, contribuendo così allo sviluppo del metodo degli indivisibili introdotto in geometria, com'è noto, da Bonaventura Cavalieri. La stretta collaborazione scientifica fra i due esimi matematici, che furono legati da profonda amicizia, è documentata da un'ampia corrispondenza scientifica.
La seconda direzione di ricerca è costituita - se ci si attiene a questa schematica classificazione - dall'applicazione della geometria allo studio del moto.

L'esperimento barometrico, che conduce all'invenzione del barometro a mercurio, e lo sviluppo delle tecniche di lavorazione dei vetri per i cannocchiali, costituiscono infine due direzioni di ricerca nelle quali Torricelli fa prova di un'abilità paragonabile a quella di un provetto artigiano.
La geometria e le sue applicazioni sono le direzioni nelle quali il genio di Torricelli si manifesta con assoluta sicurezza. L'interesse per i ragionamenti astratti va di pari passo con il rifiuto, più volte manifestato, di lasciarsi imprigionare entro i limiti ristretti di un particolare fenomeno fisico.

Io fingo - così egli scrive all'amico Michelangelo Ricci in una lettera del febbraio 1646 - o suppongo che qualche corpo o punto si muova all'ingiù e all'insù con la nota proporzione et horizzontalmente con moto equabile. Quando questo sia io dico che seguirà tutto quello che ha detto il Galileo, et io ancora. Se poi le palle di piombo, di ferro, di pietra non osservano quella supposta proporzione, suo danno, noi diremo che non parliamo di esse.
Espresse da uno scienziato che impiegava una parte notevole del suo tempo a costruire strumenti destinati allo studio di fenomeni naturali, queste osservazioni potrebbero sembrare a prima vista alquanto singolari. In realtà gli interessi di Torricelli non erano rivolti soltanto verso i ragionamenti astratti. In lui coesistevano, per così dire, due individui: il tecnico, che perfezionava i metodi pratici di fabbricazione dei vetri per cannocchiali senza preoccuparsi degli aspetti teorici del problema; il teorico del moto, che non andava volentieri alla ricerca di prove sperimentali, forse perché non credeva nella prova irrefutabile fornita dall'osservazione diretta dei fenomeni.
3.1 Cubatura dell'iperboloide di rivoluzione

(Solido iperbolico acuto)
Il metodo geometrico degli indivisibili sviluppato da Torricelli presenta una importante innovazione rispetto al metodo di Cavalieri. Il nostro metodo [...] - spiega Torricelli - procederà con gli indivisibili curvi senza seguir l'esempio di alcun predecessore [...] [Torricelli, Opere, a cura di G. Loria e G. Vassura, Faenza 1919, I (1), p. 174; tr. it. a cura di L. Belloni, Torino, UTET, 1975, p. 423]
Questa innovazione viene utilizzata da Torricelli per la dimostrazione del teorema relativo al solido iperbolico acuto, che gli permette di stabilire l'equivalenza fra il solido infinitamente lungo generato da una iperbole rotante intorno al proprio asse, ed un cilindro di altezza finita. [ibidem, I (1), pp. 193-194; tr. it. pp. 444-45].
La dimostrazione riposa su 5 lemmi:



fig. 1		 Primo lemma
Data una iperbole i cui asintoti siano AB, AC, e fatta girare la figura intorno all'asse AB, si ottiene il solido acuto iperbolico infinitamente lungo verso B (fig. 1). Si considera poi, all'interno del solido così definito, un rettangolo passante per AB, ad esempio il rettangolo DEFG. Sia AH il semiasse dell'iperbole.
Il quadrato costruito su AH ha la stessa area di qualunque  rettangolo DEFG, in virtù della definizione stessa dell'iperbole [ibidem, p. 191; tr. it. p. 442].



fig. 2		 Secondo lemma
Si dimostra che tutti i cilindri inscritti nel solido acuto iperbolico intorno all'asse comune AB (fig. 2), sono isoperimetrici, (le loro superfici laterali sono uguali) [ibidem, pp. 191-192; tr. it. pp. 442-43].



Terzo lemma
Si dimostra che i volumi di tutti i cilindri isoperimetrici sopra descritti stanno fra di loro come i diametri delle loro basi [ibidem, p. 192; tr. it., p. 443].



fig. 3		 Quarto lemma
Si dimostra che la superficie laterale del cilindro GIHL (fig. 3), è ¼ della superficie della sfera AEFC [ibidem, pp. 192-193; tr.it., p. 443-44].

Quinto lemma
Si dimostra che la superficie laterale di ogni cilindro GHIL inscritto nel solido acuto come nella precedente figura, è equivalente al cerchio di raggio DF [ibidem, p. 193; tr. it., p. 444].



fig. 4

 

 Teorema
Si dimostra che il solido infinitamente lungo FEBDC costituito dal solido acuto iperbolico EBD e dal suo cilindro di base FEDC, è equivalente al cilindro ACGH di altezza AC (fig. 4) [ibidem, pp. 193-194; tr. it., pp. 444-45]

fig. 5
Immagine tratta da L'Oeuvre de Torricelli: science galiléenne et nouvelle géométrie, publications de la faculté des lettres et sciences humaines de Nice, diff. Les Belles Lettres, Paris, 1987
 Alcune osservazioni relative alla dimostrazione
Il segmento AC = PD = altezza del cilindro ACGH, risulta dal "taglio" dell'iperbole mediante un piano perpendicolare all'asse AB (fig.4).

La dimostrazione di Torricelli riposa sul "Quinto lemma": la superficie laterale di ogni "cilindro inscritto", come ad esempio GIHL, é uguale al "cerchio di raggio DF" (fig. 3). Questa conclusione é decisiva per "costruire" il cilindro ACGH (fig.5), che Torricelli considera come l'aggregato di un numero infinito di cerchi.

Nella figura 5, la superficie laterale del cilindro OILN é uguale al cerchio passante per il punto I. Questa conclusione é vera per qualunque cilindro inscritto, ad ognuno dei quali corrisponderà un cerchio (di raggio costante DF) passante per uno degli infiniti punti del segmento AC.


3.2 Quadratura dello spazio cicloidale


La storia della curva cicloide non é facile da riassumere in poche linee. La sua invenzione risalirebbe all'inizio del XVII secolo, secondo quanto afferma Carlo Dati nella Lettera a Filaleti di Timauro Antiate. Della vera storia della cicloide, e della famosissima esperienza dell'argento vivo, pubblicata a Firenze nel 1662. Galileo, sempre secondo Dati, avrebbe studiato questa curva, di cui egli stesso per primo avrebbe avuto l'idea, intorno agli anni 1600. Questa priorità è confermata, come vedremo, dallo stesso Galileo: la scoperta si situerebbe nell'ultimo decennio del XVI secolo.
Dati cita uno scritto di Stefano Degli Angeli del 1661, De superficie ungulae, nel quale l'autore attribuisce a Galileo il merito d'aver immaginato e studiato per primo questa curva particolare e a Torricelli quello di aver calcolato per primo il valore esatto della superficie compresa fra un arco completo di cicloide e la retta fissa. Degli Angeli fonda la sua asserzione su una lettera (di cui egli possiede copia) inviata da Bonaventura Cavalieri a a Galileo il 14 febbraio 1640. Mi sono stati mandati da parigi - scrive Cavalieri - due quesiti da quei matematici circa dei quali temo di farmi poco onore. Fra i quesiti, alcuni concerno appunto la cicloide. Era stato Jean François Niceron a sottometerglieli, in occasione di un soggiorno in Italia. La risposta di Galileo, del 24 febbraio dello stesso anno, chiarisce alcuni punti: Dei quesiti mandatigli di Francia - spiega Galileo - non so che sia stato dimostrato alcuno. Gli ho con lei per difficili molto a essere sciolti. Questa linea arcuata (i.e. la cicloide, N.d.R. ) sono più di 50 anni che mi venne in mente di descriverla [...] per adattarla agli archi di un ponte [...]. Parvemi da principio che lo spazio potesse essere triplo del cerchio che lo descrive, ma non fu così, benchè la differenza non sia molta [...] Ebbi circa un anno fa una scrittura di un padre Mersenno dei Minimi di San Francesco di Paola mandatami da Parigi, ma scrittami in caratteri tali che tutta l'Accademia di Firenze non ne potesse intender tanto che se ne potesse trar costrutto alcuno [...] io risposi all'amico che me la mandò che facesse intendere al detto padre che mi scrivesse in caratteri più intelligibili.

Dati critica violentemente il contenuto di una pubblicazione (dovuta a Blaise Pascal N.d.R.) apparsa in Francia nell'ottobre del 1658, l'Histoire de la Roulette, appelée autrement la Trochoide ou la Cycloide, in cui si sostiene che il padre Marin Mersenne sia stato il primo ad immaginare, verso il 1615, la curva cicloide en considérant le roulement des roues. Dopo aver chiesto la soluzione a Galileo, Mersenne si sarebbe rivolto a Gilles Personnier de Roberval nel 1634 e questi avrebbe dimostrato che l'espace cycloidal est 3pr 2. Secondo l'autore dell'Histoire, Roberval avrebbe chiesto a Marsenne di scrivere a tutti i matematici per dir loro che la soluzione era stata trovata (da Roberval), senza tuttavia comunicarla. Più tardi, nel 1635, Mersenne avrebbe inviato la soluzione di Roberval a diversi matematici, chiedendo loro di dimostrarla. Le due sole risposte ricevute, fra di loro diverse, sarebbero state quelle di Pierre de Fermat e di René Descartes. Nel 1638, sempre secondo l'autore dell'Histoire, Jean de Beaugrand avrebbe inviato a Galileo quel che egli sapeva della soluzione, facendo in modo da apparire egli stesso come l'autore delle cose dette. Dopo la morte di Galileo, avvenuta nel gennaio del 1642, Torricelli avrebbe ritrovato, nelle carte lasciate dal Maestro, la soluzione inviata da Beaugrand nel 1638. Questa asserzione contrasta con quanto indicato da Galileo nella lettera del 24 febbraio 1640 citata.
Da sottolineare, infine, che il 23 aprile 1643 Cavalieri scrive a Torricelli e si congratula con lui per la soluzione trovata. Finalmente ho sentito - scrive Cavalieri - nell'ultima sua la misura dello spazio cicloidale con molta mia maraviglia, essendo stato sempre stimato problema di molta difficoltà, che straccò già il Galileo; ed io pure, parendomi assai difficile lo lasciai andare; ond'ella avrà non poca lode di questo, oltre le tante sue maravigliose invenzioni, che le daranno eterna fama. Non resterò poi di dirle intorno a questo, che il Galileo mi scrisse una volta d'averci applicato 40 anni fa, e che non aveva potuto trovar niente; e che s'era persuaso che il detto spazio fosse triplo del circolo suo genitore, ma che poi li pareva che non fosse precisamente, se mal non ricordo, poiché per quanto abbi cercato nelle mie scritture, non ho mai potuto tal lettera ritrovare.

Torricelli fu, senza alcun dubbio, il primo ad aver pubblicato a Firenze nel 1644 la soluzione del problema (in Opera Geometrica, «De dimensione Parabolae, solidique Hyperbolici problemata duo...», p. 85-90). Tre dimostrazioni si trovano in appendice al capitolo indicato, attraverso le quali dimostreremo - scrive Torricelli - con l'aiuto di Dio che [lo spazio cicloidale] é triplo [del cerchio generatore]. La prima e la terza dimostrazione sono condotte con il metodo degli indivisibili, la seconda alla maniera degli antichi, per doppia riduzione all'assurdo. [Torricelli, Opere, a cura di G. Loria e G. Vassura, Faenza 1919, I (1), p. 174; tr. it. a cura di L. Belloni, Torino, UTET, 1975, p. 423]

[in Torricelli,Opere, a cura di G. Loria e G. Vassura, Faenza 1919, I (1), pp. 163-169).

Torricelli indica innanzi tutto i primi tentativi empirici per misurare gli "spazi materiali" (spatijs figurarum materialibus) delimitati dalla curva cicloidale, e quindi il metodo per costruire la curva stessa.

Diamo qui di seguito il testo italiano del preambolo torricelliano nella traduzione di L. Belloni (cfr. Torricelli, Opere, Torino, UTET,1975, pp. 410-412).

APPENDICE SULLA MISURA DELLA CICLOIDE

Mi piace qui aggiungere, come appendice, la soluzione di un problema interessante che, a prima vista, sembra difficilissimo se se ne considera l'argomento e l'enunciazione. Esso tormentò e sfuggì, molti anni or sono, ai primi matematici del nostro secolo. Infatti, la dimostrazione invano cercata sfuggì dalle loro mani a causa della fallacia dell'esperienza. Appesi infatti ad una libra, costruita a mano, gli spazi materiali delle figure, non sò per quale destino, quella proporzione che in realtà  é tripla, risultò sempre meno che tripla. Avvenne allora che, sospettando trattarsi di grandezze incommesurabili (come credo io) piuttosto che disperando della soluzione, la ricerca intrapesa venne da quei matematici abbandonata.



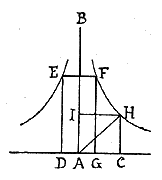
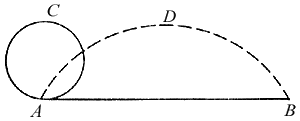
Si facciano le seguenti supposizioni. Si immagini su una retta fissa AB, il circolo AC, tangente alla retta AB nel punto A. E si fissi il punto A, sulla periferia del circolo. Allora si immagini di far ruotare il circolo AC sulla retta fissa AB, con moto insieme circolare e progressivo verso B, ed in modo che, negli istanti sucessivi, tocchi sempre la linea retta AB con un suo punto, finché il punto fissato di nuovo non torni al contatto con la linea, ad esempio in B. È certo che il punto A, fisso sulla periferia del circolo rotante AC, descriverà qualche linea, dapprima ascendente a partire dalla linea sottostante AB, poi culminante verso D, e, in ultimo, prona e discendente verso il punto B.
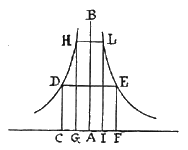
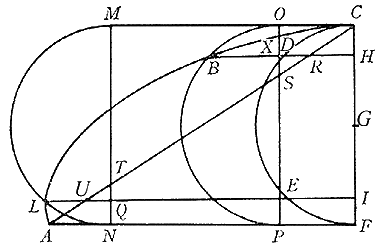
Tale linea é stata chiamata cicloide dai nostri predecessori, sopratutto da Galileo già 45 anni orsono. La retta AB é stata chiamata base della cicloide, ed il circolo AC, il generatore della cicloide.
Discende dalla natura della cicloide la proprietà che la sua base AB sia eguale alla periferia del circolo generatore AC. E questo poi non é così oscuro. Infatti tutta la periferia AC, nella sua rotazione, si é commisurata con la retta fissa AB.
Si chiede ora che proporzione ha lo spazio cicloidale ADB al suo circolo generatore AC. Dimostreremo (e ne siano rese grazie a Dio) che é triplo. Le dimostrazioni saranno tre, e del tutto diverse fra loro. La prima e la terza procederanno con la nuova geometria degli indivisibili, che a noi piace molto. Metre la seconda procederà con la duplice posizione, secondo il metodo degli antichi, onde soddisfare i fautori di entrambi i metodi. Del resto, io dico questo: quasi tutti i principi coi quali si dimostra qualcosa nella geometria degli indivisibili, si possono ridurre alla solita dimostrazione indiretta degli antichi. Ciò è stato da noi fatto, come in molti altri casi, anche nel primo e nel terzo dei seguenti teoremi. Tuttavia per non abusare troppo della pazienza del lettore, abbiamo ritenuto di tralasciare molte dimostrazioni e di darne soltanto tre.

Ci limitiamo a dare, sempre nella traduzione di Belloni ( cfr ibidem, pp. 412-413), la prima dimostrazione fatta col metodo degli indivisibili.

Teorema I

Lo spazio compreso fra la cicloide e la sua retta di base é triplo del circolo generatore. Ovvero é sesquialtero (Sesquialtero = 1+1/2 N.d.R.) del triangolo, avente la sua stessa base ed altezza.

Sia data la cicloide ABC, descritta dal punto C del circolo CDEF quando ruota sulla base fissa AF. Consideriamo la semicicloide ed il semicircolo soltanto per evitare troppa confusione nella figura. Dico che lo spazio ABCF é triplo del semicircolo CDEF. Ovvero sesquialtero del triangolo ACF.
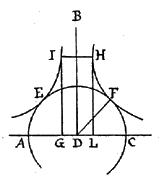
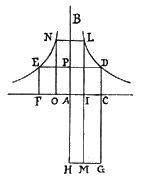
Si prendano due punti, H ed I, sul diametro CF, egualmente distanti dal centro G. Tracciate HB, IL e CM parallele a FA, passino per i punti B ed L i semicircoli OBP e MLN, eguali a CDF, tangenti alla base nei punti P ed N.


È chiaro che le rette HD, IE, XB e QL sono eguali per la proposizione 14 del libro III. Saranno eguali anche gli archi OB e LN. Analogamente, essendo eguali CH e IF, saranno eguali CR e UA, per le proprietà delle rette parallele. Tutta la periferia MLN, per la definizione stessa della cicloide, é eguale alla retta AF. Analogamente, l'arco LN é uguale alla retta AN per la medesima ragione, poiché l'arco LN si distenderà sulla retta AN. L'arco restante LM sarà dunque eguale alla retta restante NF. Per la medesima ragione, l'arco BP sarà eguale alla retta AP, e l'arco BO alla retta PF.

Ora la retta AN é uguale all'arco LN, ovvero all'arco BO, ovvero nscritto ACF, e triplo del semicircolo CDEF. E questo ecc.

 
3.3 Difesa delle leggi galileiane del moto


In quanto erede di Galileo, Torricelli dovette affrontare le critiche mosse all'opera del Maestro, in particolare da Cartesio e da Gilles Personne de Roberval. La scienza del moto esposta nei Discorsi, non era accettata da tutti. La proporzionalità degli spazi al quadrato dei tempi nel moto di caduta libera dei gravi, e la traiettoria parabolica dei proiettili non convincevano i due scienziati francesi. Esasperato dalle loro insistenze - e soprattutto dalle perentorie affermazioni di Roberval secondo cui le conclusioni avanzate da Galileo non resistevano ad una verifica sperimentale - Torricelli decise di tagliar corto ad ogni discussione.
Disegno tratto dalla Lettera
a G. B. Ranieri del Settembre
1647.



Frammento della lettera di
Torricelli a Michelangelo
Ricci del 17 gennaio 1645
relativa ai suoi lavori sulla
spirale di Archimede,
pubblicata in Opere di
Evangelista Torricelli,
a cura di G. Loria e G.Vassura,
Faenza 1919 p.257.
Egli fece notare allo scienziato francese, in una lettera del 7 Luglio 1646, che in una sua opera Archimede aveva assimilato le traiettorie dei proiettili a delle spirali. Quando l'errore fu evidente, bisognava forse condannare il libro? non era preferibile leggere il tutto senza alcun riferimento ai proiettili, aggiungendo semplicemente il vocabolo "punto", il cui moto non segue una legge naturale, ma immaginaria? In realtà, spiega Torricelli, le dimostrazioni geometriche non hanno bisogno di aiuto: esse sono autosufficienti. E conclude proponendo di buttar via dal libro di Archimede le parole "proiettili", "corpi pesanti ", "balliste", ecc., che appartengono alla fisica, e di lasciare invece le proposizioni astratte, che appartengono alla geometria.
Il tono provocatorio della lettera a Roberval non deve farci dimenticare che in realtà Torricelli credeva nella validità delle leggi del moto naturale stabilite da Galileo. Il contenuto delle lettere scambiate con Giovan Battista Renieri costituisce, in questo senso, un'importante testimonianza.Il suo rifugiarsi dietro l'aspetto astratto dei lavori sulla teoria del moto, è verosimilmente un modo per evitare le polemiche. Io poi per fuggire le controversie - scrive Torricelli a Renieri nel Settembre 1647 - apposta più volte iteratamente e chiaramente mi sono protestato nei miei libri del moto di scrivere piuttosto ai filosofi che ai bombardieri. Ma questa osservazione non gli impedisce di dare un'interpretazione delle traiettorie dei proiettili realmente osservate, e di fornire valori numerici pazientemente calcolati.
3.4 L'esperimento barometrico

L'eserienza di Gasparo Berti.
Incisione da Technica
Curiosa di P. Schott,
Herbipoli 1664.

 L'esperimento dell'argento vivo, realizzato nella primavera del 1644, renderà celebre il nome di Torricelli in Italia ed oltralpe. Il merito dello scienziato italiano fu innanzitutto di ammettere che la causa effettiva della resistenza che la natura oppone al vuoto, era dovuta probabilmente al peso dell'aria. Questa opinione, com'è noto, non era stata condivisa da Galileo. L'esperimento di Firenze ebbe quindi come motivazione iniziale la ricerca di una relazione possibile fra il peso dell'aria e la resistenza che si incontrava nel voler fare il vuoto. Un esperimento simile era già stato effettuato a Roma, probabilmente quando Galileo era ancora in vita, da Gasparo Berti in presenza dei padri gesuiti Niccolò Zucchi e Attanasio Kircher, ma i risultati furono divulgati solo nel 1647. Berti aveva utilizzato l'acqua, e quindi il tubo aveva una lunghezza di dieci metri circa. L'idea originale di Torricelli, il suo contributo tecnico all'esperimento, consistette nell'impiego del mercurio al posto dell'acqua, una innovazione questa, che permise di dividere per tredici la lunghezza del tubo. Già prima di effettuare l'esperimento, Torricelli si chiedeva se, nello scendere per venire ad equilibrare la colonna d'aria, la colonna di mercurio lasciava effettivamente dietro di sé uno spazio vuoto.


Disegno tratto dalla lettera di
Torricelli a M. Ricci del
11 Giugno 1644, pubblicata in
Opere dei Discepoli di
Galileo, Firenze 1975.

 L'esperimento di Torricelli suscitò un'eco profonda, particolarmente in Francia ed in Polonia. Le discussioni non furono sempre centrate sull'aspetto tecnico, né sulle conclusioni scientifiche che era lecito trarne, ma rilanciarono, invece, la polemica fra "antichi" e "moderni". In effetti, la caduta solamente parziale del mercurio, faceva apparire nel tubo una zona apparentemente vuota, mettendo in crisi così uno dei principi fondatori della fisica aristotelica.
I gesuiti si batterono con convinzione per difendere la non esistenza del vuoto. E' lecito chiedersi quale fu il contributo di Torricelli al dibattito. La risposta è semplice: egli non vi partecipò affatto. In due lettere indirizzate l'11 ed il 28 giugno 1644 a Michelangelo Ricci, il matematico del Granduca descrive l'esperimento, ma non prende posizione nel dibattito filosofico sollevato dall'apparizione del vuoto. Egli osserva semplicemente, nella lettera dell'11 giugno, che molti hanno detto, che il vacuo non si dia, altri che si dia, ma con repugnanza della Natura e con fatica.
E Torricelli considera che l'esperimento non è del tutto riuscito, poiché l'altezza della colonna di mercurio che doveva equilibrare il peso dell'aria, variava per il caldo e freddo. Tuttavia si poteva giungere alla conclusione che il valore del peso dell'aria proposto dagli "antichi" era del tutto errato. Altro risultato importantissimo: la forza che impediva al mercurio di cadere, non era interna al vaso; Torricelli emetteva quindi l'ipotesi, in questa stessa lettera, che essa fosse esterna e dovuta alla gravità dell'aria.
Le due lettere a Ricci sono gli unici documenti redatti dallo stesso Torricelli. Si può ipotizzare che questo silenzio sia dovuto al disappunto per l'intervento dei teologi nel dibattito. Una frase di Ricci accredita questa ipotesi. Stimo che sarà pur troppo nauseato - scrive questi in una lettera a Torricelli del 18 giugno 1644 - dalla temeraria opinione de' suddetta Teologi, e dal costume suo costante di meschiar subito le cose di Dio ne' ragionamenti naturali, dove che quelle dovrebbono con maggior rispetto, e riverenza esser trattate. I motivi dell'intervento nel dibattito di eminenti personalità della Chiesa romana sono complessi ed ancor oggi non del tutto elucidati. Si può tuttavia osservare che per i difensori della tradizione aristotelico-tomista, l'esistenza del vuoto, che andava di pari passo con quella degli atomi, permetteva di far riferimento alla filosofia di Leucippo, Democrito ed Epicuro